初步理解
流形manifold是高维空间中曲面、曲线概念的扩展。 我们可以在低维上直观理解这个概念， 比如我们说三维空间中的一个曲面是一个二维流形， 因为它的本质维度（intrinsic dimension）只有2， 一个点在这个二维流形上移动只有两个方向的自由度。 同理，三维空间或者二维空间中的一条曲线都是一个一维流形。
维基百科图例
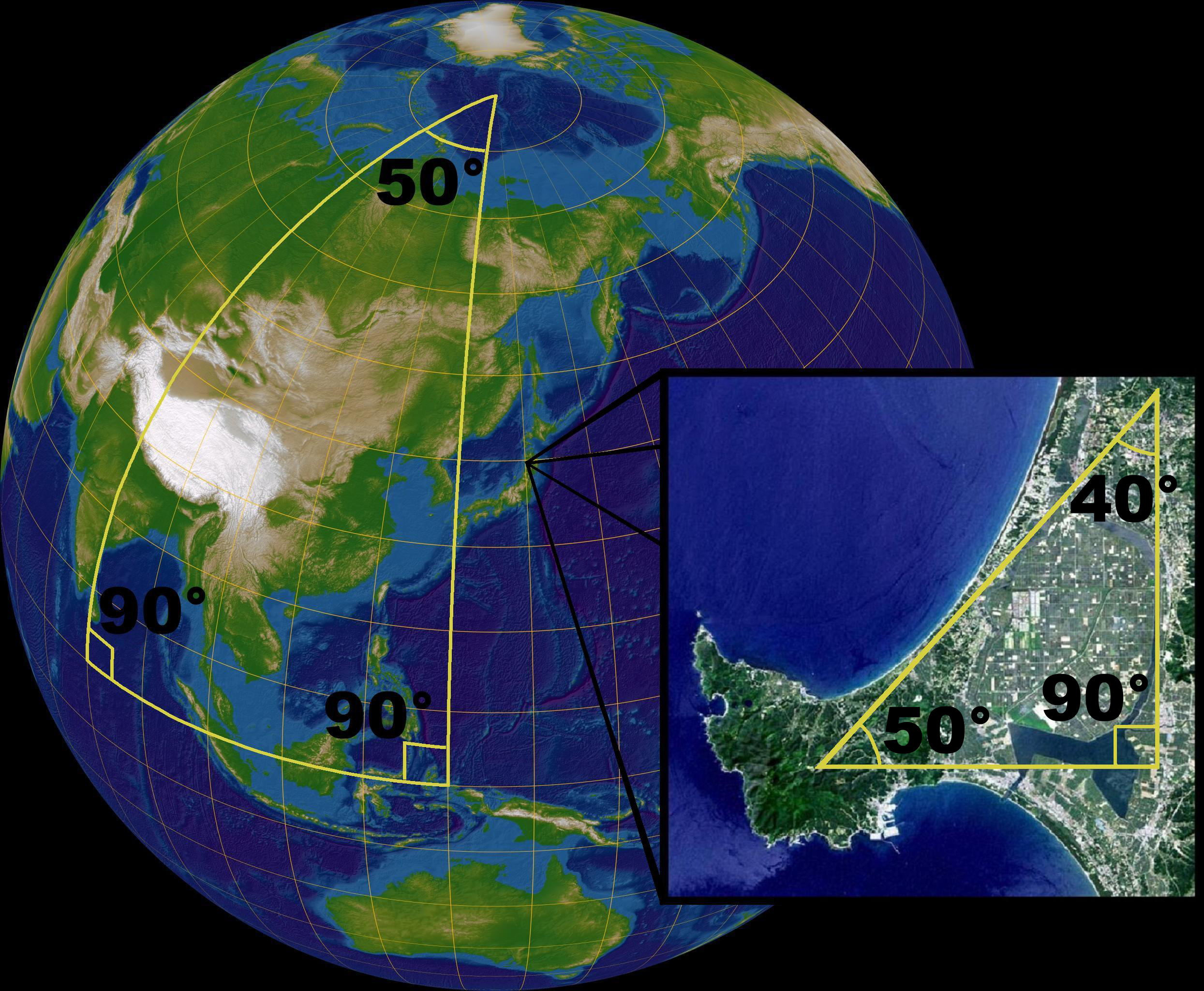球面（球的表面）为二维的流形，由于它能够由一群二维的图形来表示。
进一步理解
同在欧几里德空间里一样，流形也是有维度的，这个维度在局部里定义。 如果流形的图是n维的，那么这个图被称为n维流形。 比如球面的任意一个细小的局部是一个2维平面，那么球面就是一个2维流形。 从以上例子也可以看出，流形的维度同它在欧几里德空间的个体（3维）比较是下降了。 直观来看，因为在曲面上的运动本来就也只有两个自由度。 通常对于笛卡儿坐标系的曲面，可以找到对应的低维度流形坐标，这个过程叫做参数化（Parameterization）。
